La serie de Taylor de una función f de números reales o complejos que es infinitamente diferenciable en un entorno de números reales o complejos a, es la serie de potencias
que puede ser escrito de una manera más compacta como
donde n! es el factorial de n y f (n)(a) denota la n-ésima derivada de f en el punto a; la derivada cero de f es definida como la propia f y (x − a)0 y 0! son ambos definidos como uno.
A continuación se enumeran algunas series de Taylor de funciones básicas. Todos los desarrollos son también válidos para valores complejos dex.
Función exponencial y logaritmo natural
Serie geométrica
Teorema del binomio
paray cualquier
complejo
Funciones trigonométricas
-
- Donde Bs son los Números de Bernoulli.
Funciones hiperbólicas
Función W de Lambert
Los números Bk que aparecen en los desarrollos de tan(x) y tanh(x) son Números de Bernoulli. Los valores C(α,n) del desarrollo del binomio son los coeficientes binomiales. Los Ek del desarrollo de sec(x) son Números de Euler.


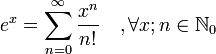


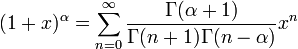

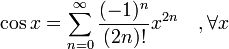









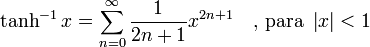





La fuente bibliográfica?
ResponderEliminarx2
ResponderEliminarx3
ResponderEliminarKarla,M,C(24 de mayo 2011)
ResponderEliminarBuen aporte
ResponderEliminarLas series de Taylor de funciones básicas también pueden contarse como los tipos de representaciones de la serie de Tylor o no?
ResponderEliminarJIJIJIJA
ResponderEliminar