CALCULO INTEGRAL: 4.1.2 infinitas (Criterio de d'alembert y criterio de ), 4.1.1 finita, 4.1 definicion de serie

4.1.2 infinit (Criterio de d'alembert y criterio de ), 4.1.1 finita, 4.1 definicion de serie

4.1 Definicion de serie
Definiciones y notación.

A la suma de una sucesión de términos se denomina SERIE y el valor de dicha suma, si es que tiene
alguno, se define como

S = lim S n .
n→∞
Un ejemplo de serie infinita, denominada así debido a que dicha sucesión es infinita, es la
denominada serie geométrica, la cual se obtiene a partir de un térmno inicial
multiplicado por una cantidad constante, p. ej.
a + ar + ar 2 + ar 3 + ⋅ ⋅ ⋅ + ar n −1 + ⋅ ⋅ ⋅ . En
este caso la cantidad inicial a es multiplicada por la cantidad constante r para obtener dicha
serie infinita.
En general una serie infinita significa una expresión de la forma
a1 + a2 + a3 + ⋅ ⋅ ⋅ + an + ⋅ ⋅ ⋅ ,
donde las an son números o funciones dadas por alguna regla o fórmula. Los tres puntos
significan que la serie nunca termina. Si se tiene duda de cómo es la regla usada en la
formación e la serie, el término general o término n-ésimo deberá expresarse, p. ej.
12 + 2 2 + ⋅ ⋅ ⋅ + n 2 + ⋅ ⋅ ⋅
x − x 2 + x
2
+ ⋅ ⋅ ⋅ +
(− 1)n−1 x n
(n − 1)!
+ ⋅ ⋅ ⋅
También usaremos formas abreviadas para denotar las series, p. ej. para las series anteriores, la
forma abreviada será

∞
∑
n=1
∞
∑ n 2
n =1
(− 1)n−1 x n
(n − 1)! .

Las aplicaciones de las series infinitas son muchas, pero mencionamos como lo más importante para
nosotros en este momentos, su uso en la solución de problemas matemáticos que no pueden resolverse
en términos de funciones elementales ( potencias, raíces, funciones trigonométricas y sus inversas,
logaritmos y exponenciales y combinaciones de estos), o en caso de que puedan resolverse, es muy
complicado trabajar con ellos. En estos casos encontramos una respuesta en función de una serie y
usamos
los términos requeridos de acuerdo a la presición deseada. Las ecuaciones diferenciales son
resueltas en muchas ocasiones en función de series infinitas. Una integral definida,
0.1
por ejemplo,
∫ e − x
0
dx , para la cual no hay solución en términos de funciones
elementales, se puede resolver su expandiendo su integrando en una serie e integrando término a
término dicha serie.

4.1.1

Finitas

Una diferencia finita es una expresión matemática de la forma f(x + b) − f(x +a). Si una diferencia finita se divide por b − a se obtiene una expresión similar al cociente diferencial, que difiere en que se emplean cantidades finitas en lugar de infinitesimales. La aproximación de las derivadas por diferencias finitas desempeña un papel central en los métodos de diferencias finitas del análisis numérico para la resolución deecuaciones diferenciales.

La diferencia anterior puede considerarse un operador diferencial que hace corresponder la función f con Δf. El teorema de Taylor puede expresarse por la fórmula

$\Delta = hD + \frac12 h^2D^2 + \frac1{3!} h^3D^3 + \cdots = \mathrm{e}^{hD} - 1,$

Donde D denota el operador derivada, que hace corresponder $f\,$ con su derivada $f\,'$ , es decir, $D = u'\,, D^2 = u''\,, D^3 = u'''\,,...$

Formalmente, invirtiendo la exponencial,

$hD = \log(1+\Delta) = \Delta - \frac12 \Delta^2 + \frac13 \Delta^3 + \cdots. \,$

Esta fórmula sigue siendo válida en el sentido de que ambos operadores dan el mismo resultado cuando se aplican a un polinomio. Incluso para funciones analíticas, las series de la derecha no convergen con seguridad, sino que puede tratarse de una serie asintótica. Sin embargo, pueden emplearse para obtener aproximaciones más precisas de la derivada. Por ejemplo, Los dos primeros términos de la serie llevan a:

$f'(x) \approx \frac{\Delta[f](x) - \frac12 \Delta^2[f](x)}{h} = - \frac{f(x+2h)-4f(x+h)+3f(x)}{2h}.$

El error de la aproximación es del orden de h².

Las fórmulas análogas para los operadores posterior y central son

$hD = -\log(1-\Delta) \quad\mbox{y}\quad hD = \, \operatorname{arcsinh} \left( \Delta \right).$

4.1.2 Criterio de D'Alembert o Criterio del Cociente (Criterio de la razón)

Sea una serie $\sum_{k=1}^{\infty} a_k$ , tal que

a k > 0

( serie de términos positivos).

Si existe

$\lim_{k \rightarrow \infty} \frac {a_k}{a_{k-1}}=L$

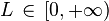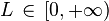con $L \, \in \, [0, +\infty)$ , el Criterio de D'Alembert establece que:

si $L < 1$ , la serie converge.
si $L > 1$ , entonces la serie diverge.
si $L = 1$ , no es posible decir algo sobre el comportamiento de la serie.

En este caso, es necesario probar otro criterio, como el criterio de Raabe.

Criterio de Cauchy (raíz enésima)

Sea una serie $\sum_{k=1}^{\infty} a_k$ , tal que

a k > 0

(serie de términos positivos). Y supongamos que existe

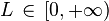
$\lim_{k \rightarrow \infty} \sqrt [k] {a_k}=L$ , siendo $L \, \in \, [0, +\infty)$

Entonces, si:

$L < 1$ , la serie es convergente.
$L > 1$ entonces la serie es divergente.
$L$ =1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe, o de comparación, para ver si podemos llegar a alguna conclusión.

CALCULO INTEGRAL

lunes, 6 de junio de 2011

4.1.2 infinitas (Criterio de d'alembert y criterio de ), 4.1.1 finita, 4.1 definicion de serie

4.1.2 infinit (Criterio de d'alembert y criterio de ), 4.1.1 finita, 4.1 definicion de serie

4.1.1

4.1.2

Criterio de D'Alembert o Criterio del Cociente (Criterio de la razón)

Criterio de Cauchy (raíz enésima)

1 comentario: